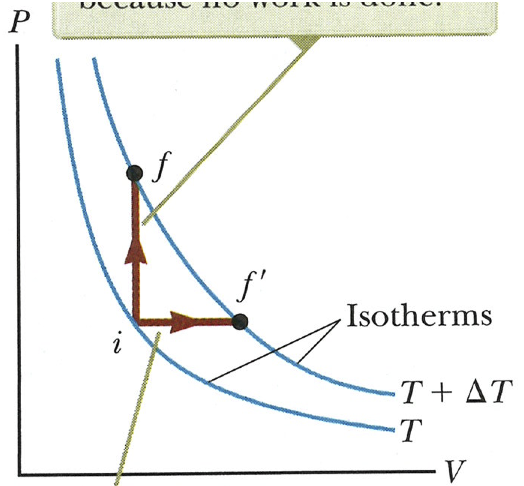
On the P-V diagram, two processes are shown. For each one discuss whether Q, W, and ΔEint are positive, negative, or zero.
Reading assignment: 21.2-21.4

On the P-V diagram, two processes are shown. For each one discuss
whether Q, W, and ΔEint are positive,
negative, or zero.
In both cases deltaE is positive because the system moves to a higher temperature isotherm. In the isovolumetric case no work is done so W = 0. Because deltaE is positive and W = 0, Q must be positive and equal to deltaE (by the First Law, Q = deltaE - W). In the isobaric case, work done *on* the system is negative (it expanded---the gas did work on its surroundings). Again, deltaE is positive. Using the First Law again (Q = deltaE - W), Q is a positive number minus a negative number, which is always positive.
Near the end of section 21.3 (page 608 in the 8th edition of our
text), the book talks about "taking the total differential." What does
that mean? (Doing this is another acquired skill that is good to practice.)
It means that you don't assume that any of the variables (P, V, and T) are constant while you do "implicit differentiation" (at least, that's the phrase I learned). Note that the answer follows the product rule that you know from calculus: d/dT of (PV) is P*dV/dT + V*dP/dT.
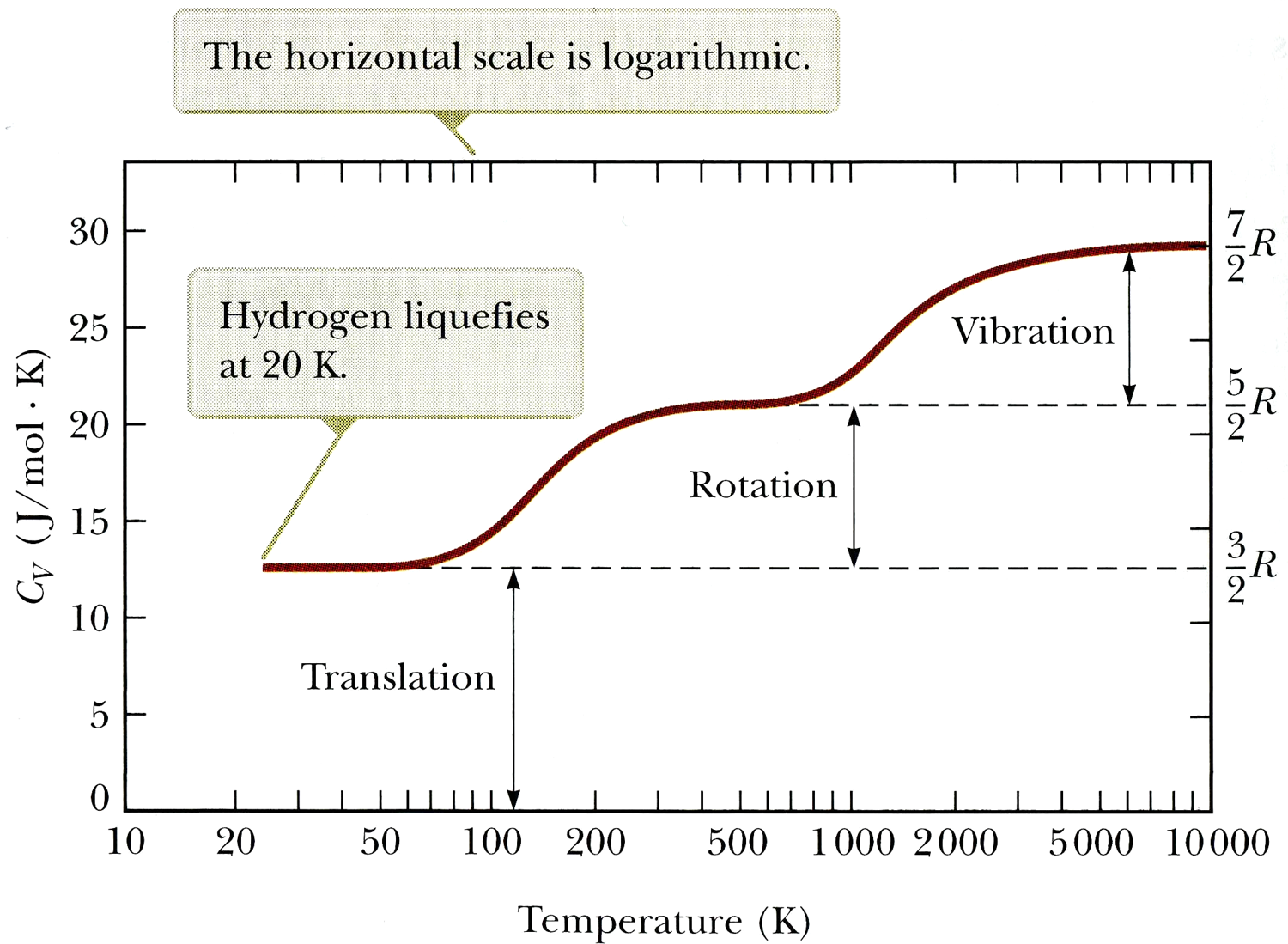
Explain why some modes (vibrational or rotational) do not contribute
to the specific heat except at higher temperatures.
Quantum weirdness. Energy can only be absorbed in fixed amounts (quanta), so some modes cannot be excited until higher temperatures make larger quanta more likely to be absorbed. More on this in physics 222...