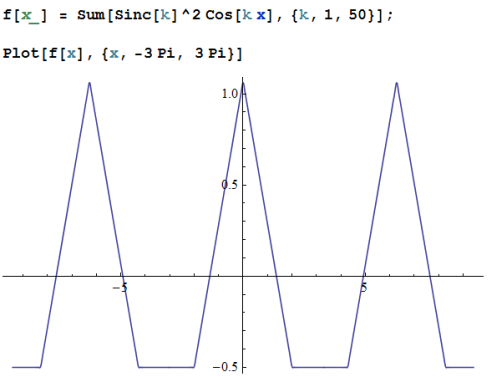
When you Fourier transform a function, the result is a sum of sines and cosines. The picture above shows one possible result. For this case, the sum is of cosines only, and the amplitudes (the "coefficients") of the cosine terms mainly decrease from one term to the next. The decrease is given by the "Sinc[k]^2" term multiplying the Cos[kx] term. ("Sinc[k]" means "(1/k) Sin[k]", in case you haven't seen that before.) Type the above code into Mathematica (use Remote Desktop Connection if it's not convenient to go to the computer lab). Verify that this particular sum does yield the periodic "tent" function shown. Play around with other forms for the coefficients. For example, try things like 1/k^2, 1/k, exp(-k). Try using only odd (or even) values of k. (You can do that by specifying a step size in the Sum command, such as {k,1,50,2}... that will only sum the odd terms.) Write down the formula for the most interesting function that you created.