Coherent Motion in a Consensus/Frustration Model

Manuel Berrondo
Wesley Krueger
Brigham Young University
Provo, Utah

Introduction

Several researchers have developed models exhibiting coherent motion among several particles (boids) based on the application of simple rules. The emergence of such complex behavior is of interest to physicists, biologists, and many other disciplines alike. These models have shown that communication among interacting particles is fundamental to their ability to move as a group, while other rules of motion determine the exact form of that movement.

We have developed a model that uses the concepts of consensus and frustration to establish highly complex and varied patterns of motion that may form an important basis for the movement of large groups of living organisms such as birds and fish. While either of these elements alone may account for certain aspects of coherent motion, we have discovered that both are required to achieve the complex patterns observed.

The Model

Our model consists of a group of particles (boids) whose interactions and subsequent movements are based on the application of two simple rules, which we have termed consensus and frustration.

Consensus

It is generally accepted that in order for a flock or school of organisms to exhibit any sort of coherent motion, each individual must in some way imitate or follow a determined group of flockmates. Biologists have also shown that within such a grouping, in general, each individual is simultaneously a leader and a follower--that is, no specific individual can be clearly classified as the leader of the flock, herd, or school, but each individual is also basing its movements upon those made by one or more of the surrounding individuals.

The question of "who follows whom" is a fundamental question in biological studies, and is a key factor in the richness of motion we have produced in our model. Many flocking models use radial proximity to determine whether or not a given individual will follow another; thus members of the group outside a given radius for a particular individual will have little to no influence on the motion of that individual. There is much biological and empirical evidence to support this type of behavior.

However, recent studies of birds have proposed that in some flocks, individual motion is not influenced so much by flockmates within a given radius as by the motions of a fixed number of flockmates regardless of their physical location within the flock. This means that a given individual may not be following those closest to it, but rather may be moving based on the influence of flockmates significantly further away.

This is the method we have used in our model and can be illustrated as follows:

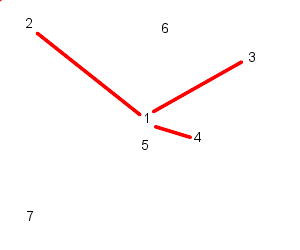Particle 1 follows 2, 3, and 4	While particle 2 follows, 3, 4, and 5
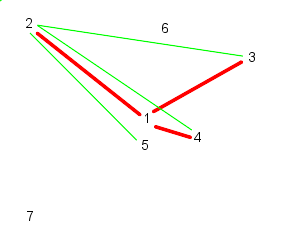
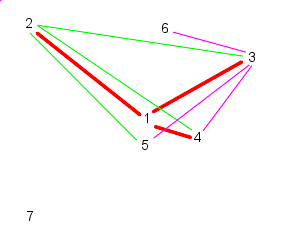3 follows, 4, 5, and 6	And 4 follows, 5, 6, and 7
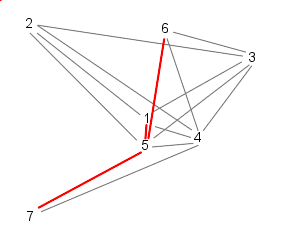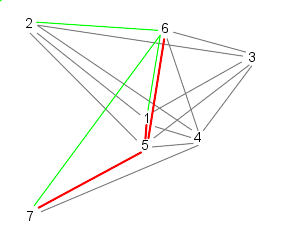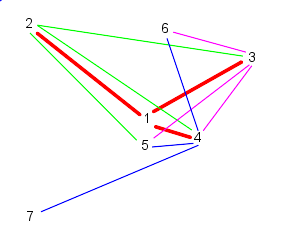
Because 7 is the last particle (in this case),  particle 5 follows 6, 7, and 1	Similarly, 6 follows 7, 1, and 2
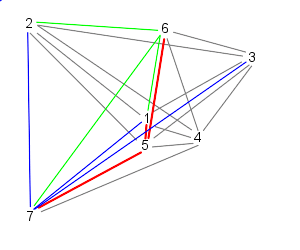Finally, particle 7 follows particles 1, 2, and 3, starting the cycle over

In our model, each individual attempts to move in the average direction of a fixed number of flockmates, which gives rise to two basic types of coherent motion:

Straight-Line Motion:

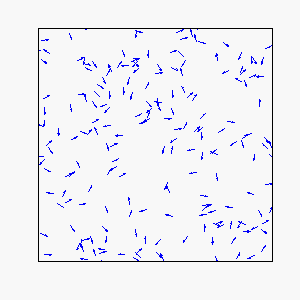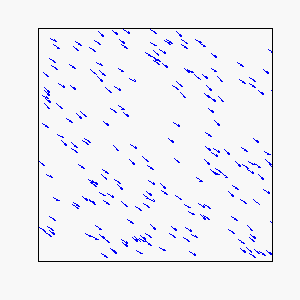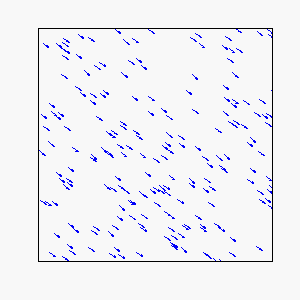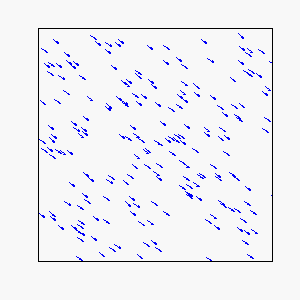
Circular Motion:

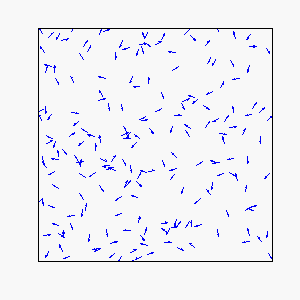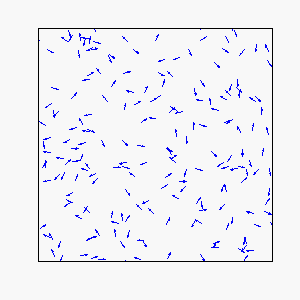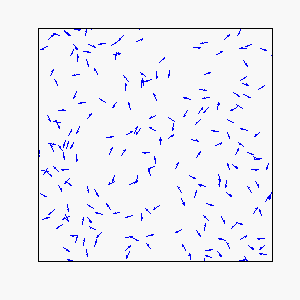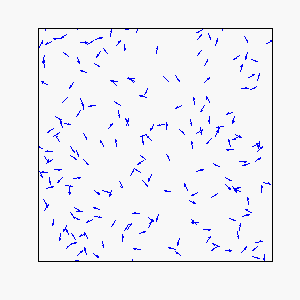
Frustration

A strict consensus model will invariably lead to uniform motion, due to the fact that the influence of neighboring particles serves as a correcting influence on all other particles. It is interesting to note that for large flocks, in which each boid is influenced by a large number of flockmates, coherent motion is achieved after only a few iterations.

Observation of large, interacting groups in nature reveals that, while their motion is coherent, it is not at all uniform, thus there seem to be other factors besides interaction with flockmates that influence each individual's behavior. In our model, this second factor has been termed frustration.

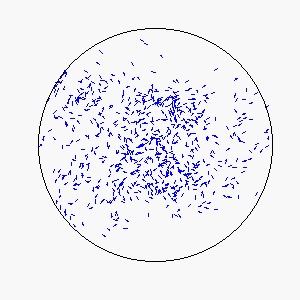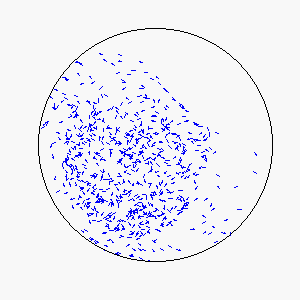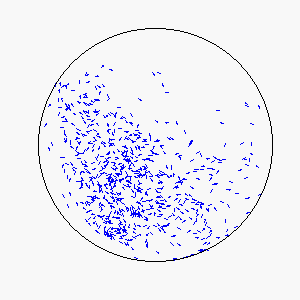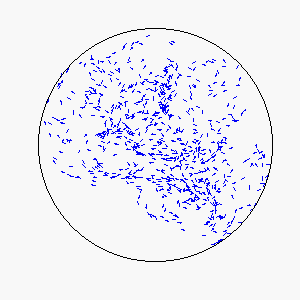
We define frustration as an influence external to the flock itself that serves to counter the uniformity of consensus-induced motion. In theory, sources of frustration may be attractive or repulsive, and may work on individuals simultaneously or asynchronously. Our model uses a basin of attraction that causes individual particles to spontaneously reverse direction upon approaching a circular boundary that can be made softer or more defined by means of the basin function. Thus, a particle approaching the boundary will be subject to a probability of reversing direction according to its position within the basin of attraction: particles near the center experience little to no probability of reversing direction, while particles near the boundary experience a very high probability of reversing direction.

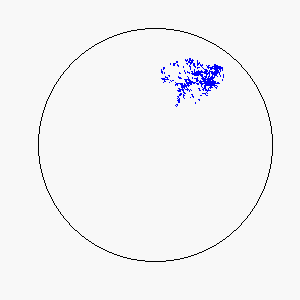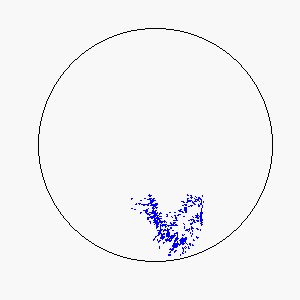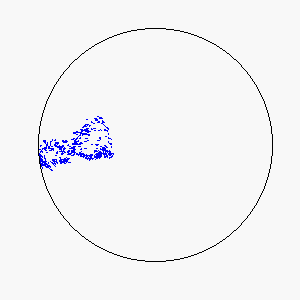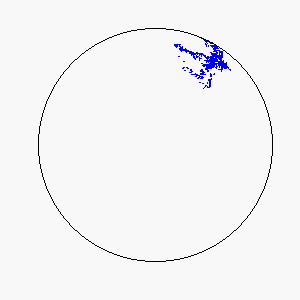
The combination of these two rules gives rise to a highly complex set of dynamic structures, similar in many ways to large groups of living organisms.

A selection of these structures is shown below: