Superluminal Light Pulse Propagation
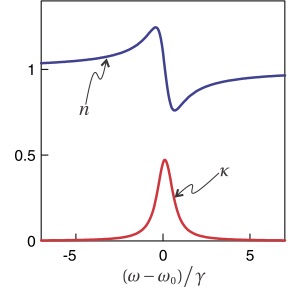
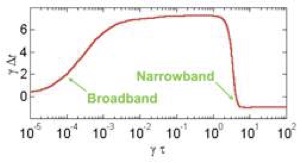
Group velocity describes pulse propagation even in situations where the pulse motion appears to exceed the speed of light in vacuum or where it becomes negative (i.e. exiting before entering). Such phenomena can occur when the spectrum of an electromagnetic pulse lies near absorption or amplifying resonance lines in the medium. Traditionally, group velocity has been understood only in the narrowband limit (i.e. for long smooth pulses in time).
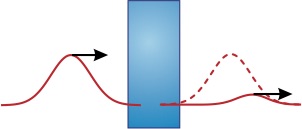
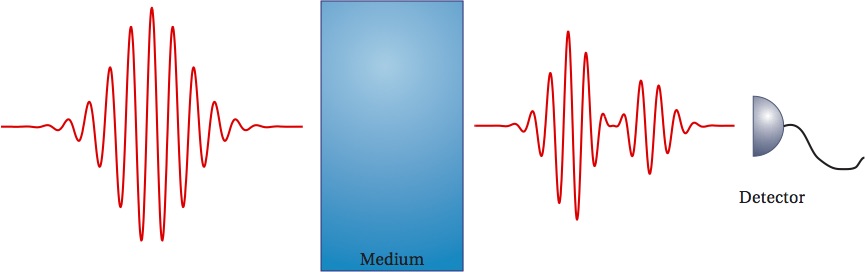
| We developed a context wherein group velocity retains meaning, even for broadband pulses (i.e. arbitrarily short duration), which can undergo severe distortion en route. In this case, a linear spectral superposition of group delay tracks the center of the field energy. This has since been confirmed experimentally. The theorem makes it obvious why short-duration pulses do not propagate superluminally and why long-duration pulses cannot propagate superluminally for distances on a scale longer than their duration. |  |
Movies
- On-Resonant Narrowband and Broadband Pulses Traversing an Absorptive Medium
- Off-Resonant Narrowband and Broadband Pulses Traversing an Amplifying Medium
Instantaneous Spectrum
So-called superluminal behavior is an artifact of paying attention only to the field energy while ignoring energy transferred into and out of the medium. We showed that a linear dielectric medium responds to the instantaneous spectrum of the field, that is, the spectrum experienced by the medium up to each moment in time. This causes the medium to exchange energy with the front of a pulse differently than with the back, which is the reason for superluminal behavior.
| In the following animation, an off resonant narrowband pulse traverses an amplifying medium. The instantaneous spectrum experienced by a point on the front of the medium is also shown. Amplification takes place for frequencies overlaping with the resonance indicated by the red vertical line. Early on, the instantaneous spectrum accesses the amplifying resonance, even though the spectrum of the whole pulse does not overlap. The black dot shows the average position of all energy (in the pulse and in the medium), which is strictly bounded by c. | 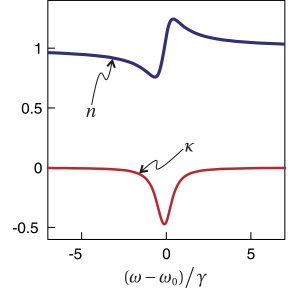 |
Movie
Group Velocity and Gratings
Our formulation is also well suited for analyzing the propagation of ultrashort pulses between a grating pair.