Demo

This paper presents a procedure for estimating the systems state when considerable Information and Communication Technology (ICT) component outages occur, leaving entire system areas un-observable. For this task, a novel method for analyzing system observability is proposed based on the Manifold Boundary Ap-proximation Method (MBAM). By utilizing information geome-try, MBAM analyzes boundaries of models in data space, thus detecting unidentifiable system parameters and states based on available data. This approach extends local, matrix-based meth-ods to a global perspective, making it capable of detecting both structurally unidentifiable parameters as well as practically uni-dentifiable parameters (i.e., identifiable with low accuracy). Be-yond partitioning identifiable/unidentifiable states, MBAM also reduces the model to remove reference to the unidentifiable state variables. To test this procedure, cyber-physical system (CPS) simulation environments are constructed by co-simulating the physical and cyber system layers.

Many systems can be modeled as an intricate network of interacting components. Often the level of detail in the model exceeds the richness of the available data, makes the model difficult to learn, or makes it difficult to interpret. Such models can be improved by reducing their complexity. If a model of a network is very large, it may be desirable to split it into pieces and reduce them separately, recombining them after reduction. Such a distributed procedure would also have other advantages in terms of speed and data privacy. We discuss piecemeal reduction of a model in the context of the Manifold Boundary Approximation Method (MBAM), including its advantages over other reduction methods. MBAM changes the model reduction problem into one of selecting an appropriate element from a partially ordered set (poset) of reduced models. We argue that the prime factorization of this poset provides a natural decomposition of the network for piecemeal model reduction via MBAM. We demonstrate on an example network and show that MBAM finds a reduced model that introduces less bias than similar models with randomly selected reductions.

Modeling outdoor environmental sound levels is a challenging problem. This paper reports on a validation study of two continental-scale machine learning models using geospatial layers as inputs and the summer daytime A-weighted L-50 as a validation metric. The first model was developed by the National Park Service while the second was developed by the present authors. Validation errors greater than 20 dBA are observed. Large errors are attributed to limited acoustic training data. Validation environments are geospatially dissimilar to training sites, requiring models to extrapolate beyond their training sets. Results motivate further work in optimal data collection and uncertainty quantification.

This chapter reviews the history, key developments in instrumentation and data analysis and representative applications of titration calorimetry to the simultaneous determination of equilibrium constants, enthalpy changes and stoichiometries for reactions in solution. Statistical methods for error analysis and optimizing operating conditions are developed and illustrated. Examples of applications of titration calorimetric methods to solve problems in biophysics are presented.

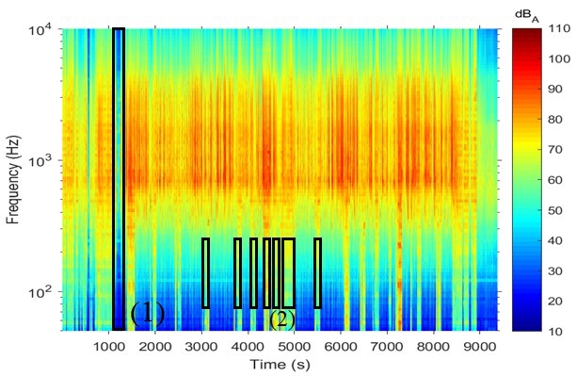
Outdoor acoustic data often include non-acoustic pressures caused by atmospheric turbulence, particularly below a few hundred Hz in frequency, even when using microphone windscreens. This paper describes a method for automatic wind-noise classification and reduction in spectral data without requiring measured wind speeds. The method finds individual frequency bands matching the characteristic decreasing spectral slope of wind noise. Uncontaminated data from several short-timescale spectra can be used to obtain a decontaminated long-timescale spectrum. This method is validated with field-test data and can be applied to large datasets to efficiently find and reduce the negative impact of wind noise contamination.

Jones et al. [J. Acoust. Soc. Am. 146, 2912 (2019)] compared an elevated (1.5 m) acoustical measurement configuration that used a standard commercial windscreen for outdoor measurements with a ground-based configuration with a custom windscreen. That study showed that the ground-based measurement method yielded superior wind noise rejection, presumably due to the larger windscreen and lower wind speeds experienced near the ground. This study further examines those findings by attempting to decouple the effects of windscreens and microphone elevation using measurements at 1.5 m and near the ground with and without windscreens. Simultaneous wind speed measurements at 1.5 m and near the ground were also made for correlation purposes. Results show that the insertion of the custom windscreen reduces wind noise more than placing the microphone near the ground, and that the ground-based setup is again preferable for obtaining broadband outdoor acoustic measurements.

This paper describes a data-driven symbolic regression identification method tailored to power systems and demonstrated on different synchronous generator (SG) models. In this work, we extend the sparse identification of nonlinear dynamics (SINDy) modeling procedure to include the effects of exogenous signals (measurements), nonlinear trigonometric terms in the library of elements, equality, and boundary constraints of expected solution. We show that the resulting framework requires fairly little in terms of data, and is computationally efficient and robust to noise, making it a viable candidate for online identification in response to rapid system changes. The SINDy-based model identification is integrated with the manifold boundary approximation method (MBAM) for the reduction of the differential-algebraic equations (DAE)-based SG dynamic models (decrease in the number of states and parameters). The proposed procedure is illustrated on an SG example in a real-world 441-bus and 67-machine benchmark.

The paper describes a manifold learning-based algorithm for big data classification and reduction, as well as parameter identification in real-time operation of a power system. Both black-box and gray-box settings for SCADA- and PMU-based measurements are examined. Data classification is based on diffusion maps, where an improved data-informed metric construction for partition trees is used. Data classification and reduction is demonstrated on the measurement tensor example of calculated transient dynamics between two SCADA refreshing scans. Interpolation/extension schemes for state extension of restriction (from data to reduced space) and lifting (from reduced to data space) operators are proposed. The method is illustrated on the single-phase Motor D example from very detailed WECC load model, connected to the single bus of a real-world 441-bus power system.

Although often ignored in first-principles studies of material behavior, electronic free energy can have a profound effect in systems with a high-temperature threshold for kinetics and a high Fermi-level density of states (DOS). Nb₃Sn and many other members of the technologically important A15 class of superconductors meet these criteria. This is no coincidence: both electronic free energy and superconducting transition temperature Tc are closely linked to the electronic density of states at the Fermi level. Antisite defects are known to have an adverse effect on Tc in these materials because they disrupt the high Fermi-level density of states. We observe that this also locally reduces electronic free energy, giving rise to large temperature-dependent terms in antisite defect formation and interaction free energies. This work explores the effect of electronic free energy on antisite defect behavior in the case of Nb₃Sn. Using ab initio techniques, we perform a comprehensive study of antisite defects in Nb₃Sn, and find that their effect on the Fermi-level DOS plays a key role determining their thermodynamic behavior, their interactions, and their effect on superconductivity. Based on our findings, we calculate the A15 region of the Nb-Sn phase diagram and show that the phase boundaries depend critically the electronic free energy of antisite defects. In particular, we show that extended defects such as grain boundaries alter the local phase diagram by suppressing electronic free-energy effects, explaining experimental measurements of grain boundary antisite defect segregation. Finally, we quantify the effect of antisite defects on superconductivity with the first ab initio study of Tc in Nb₃Sn as a function of composition, focusing on tin-rich compositions observed in segregation regions around grain boundaries. As tin-rich compositions are not observed in bulk, their properties cannot be directly measured experimentally; our calculations therefore enable quantitative Ginzburg-Landau simulations of grain boundary superconductivity in Nb₃Sn. We discuss the implications of these results for developing new growth processes to improve the properties of Nb₃Sn thin films.

We study mechanisms of vortex nucleation in Nb₃Sn superconducting RF (SRF) cavities using a combination of experimental, theoretical, and computational methods. Scanning transmission electron microscopy imaging and energy dispersive spectroscopy of some Nb3Sn cavities show Sn segregation at grain boundaries in Nb₃Sn with Sn concentration as high as ∼35 at. % and widths ∼3 nm in chemical composition. Using ab initio calculations, we estimate the effect excess tin has on the local superconducting properties of the material. We model Sn segregation as a lowering of the local critical temperature. We then use time-dependent Ginzburg-Landau theory to understand the role of segregation on magnetic vortex nucleation. Our simulations indicate that the grain boundaries act as both nucleation sites for vortex penetration and pinning sites for vortices after nucleation. Depending on the magnitude of the applied field, vortices may remain pinned in the grain boundary or penetrate the grain itself. We estimate the superconducting losses due to vortices filling grain boundaries and compare with observed performance degradation with higher magnetic fields. We estimate that the quality factor may decrease by an order of magnitude (10¹⁰ to 10⁹) at typical operating fields if 0.03% of the grain boundaries actively nucleate vortices. We additionally estimate the volume that would need to be filled with vortices to match experimental observations of cavity heating.

This paper describes the development of an automated classification algorithm for detecting instances of focused crowd involvement present in crowd cheering. The purpose of this classification system is for situations where crowds are to be rewarded for not just the loudness of cheering, but for a concentrated effort, such as in Mardi Gras parades to attract bead throws or during critical moments in sports matches. It is therefore essential to separate non-crowd noise, general crowd noise, and focused crowd cheering efforts from one another. The importance of various features—both spectral and low-level audio processing features—are investigated. Data from both parades and sporting events are used for comparison of noise from different venues. This research builds upon previous clustering analyses of crowd noise from collegiate basketball games, using hierarchical clustering as an unsupervised machine learning approach to identify low-level features related to focused crowd involvement. For Mardi Gras crowd data we use a continuous thresholding approach based on these key low-level features as a method of identifying instances where the crowd is particularly active and engaged.

The paper explores interleaved and coordinated refinement of physicsand data-driven models in describing transient phenomena in large-scale power systems. We develop and study an integrated analytical and computational data-driven gray box environment needed to achieve this aim. Main ingredients include computational differential geometry-based model reduction, optimization-based compressed sensing, and a finite approximation of the Koopman operator. The proposed two-step procedure (the model reduction by differential geometric (information geometry) tools, and data refinement by the compressed sensing and Koopman theory based dynamics prediction) is illustrated on the multi-machine benchmark example of IEEE 14-bus system with renewable sources, where the results are shown for doubly-fed induction generator (DFIG) with local measurements in the connection point. The algorithm is directly applicable to identification of other dynamic components (for example, dynamic loads).

This paper proposes a probabilistic extension to flexible hybrid state estimation (FHSE) for cyber-physical systems (CPSs). The main goal of the algorithm is improvement of the system state tracking when realistic communications are taken into account, by optimizing information and communication technology (ICT) usage. These advancements result in: 1) coping with ICT outages and inevitable irregularities (delay, packet drop and bad measurements); 2) determining the optimized state estimation execution frequencies based on expected measurement refresh times. Additionally, information about CPSs is gathered from both the phasor measurement units (PMU) and SCADA-based measurements. This measurement transfer introduces two network observability types, which split the system into observable (White) and unobservable (Grey) areas, based on 1) deployed measuring instruments (MIs) and 2) received measurements. A two-step bad data detection (BDD) method is introduced for ICT irregularities and outages. The proposed algorithm benefits are shown on two IEEE test cases with time-varying load/generation: 14-bus and 300-bus.

Outdoor ambient acoustical environments may be predicted through machine learning using geospatial features as inputs. However, collecting sufficient training data is an expensive process, particularly when attempting to improve the accuracy of models based on supervised learning methods over large, geospatially diverse regions. Unsupervised machine learning methods, such as K-Means clustering analysis, enable a statistical comparison between the geospatial diversity represented in the current training dataset versus the predictor locations. In this case, 117 geospatial features that represent the contiguous United States have been clustered using K-Means clustering. Results show that most geospatial clusters group themselves according to a relatively small number of prominent geospatial features. It is shown that the available acoustic training dataset has a relatively low geospatial diversity because most training data sites reside in a few clusters. This analysis informs the selection of new site locations for data collection that improve the statistical similarity of the training and input datasets.

The paper describes a data-driven system identification method tailored to power systems and demonstrated on models of synchronous generators (SGs). In this work, we extend the recent sparse identification of nonlinear dynamics (SINDy) modeling procedure to include the effects of exogenous signals and nonlinear trigonometric terms in the library of elements. We show that the resulting framework requires fairly little in terms of data, and is computationally efficient and robust to noise, making it a viable candidate for online identification in response to rapid system changes. The proposed method also shows improved performance over linear data-driven modeling. While the proposed procedure is illustrated on a SG example in a multi-machine benchmark, it is directly applicable to the identification of other system components (e.g., dynamic loads) in large power systems.

We use time-dependent Ginzburg-Landau theory to study the nucleation of vortices in type-II superconductors in the presence of both geometric and material inhomogeneities. The superconducting Meissner state is metastable up to a critical magnetic field, known as the superheating field. For a uniform surface and homogeneous material, the superheating transition is driven by a nonlocal critical mode in which an array of vortices simultaneously penetrate the surface. In contrast, we show that even a small amount of disorder localizes the critical mode and can have a significant reduction in the effective superheating field for a particular sample. Vortices can be nucleated by either surface roughness or local variations in material parameters, such as 

T

c

. Our approach uses a finite-element method to simulate a cylindrical geometry in two dimensions and a film geometry in two and three dimensions. We combine saddle-node bifurcation analysis along with a fitting procedure to evaluate the superheating field and identify the unstable mode. We demonstrate agreement with previous results for homogeneous geometries and surface roughness and extend the analysis to include variations in material properties. Finally, we show that in three dimensions, surface divots not aligned with the applied field can increase the superheating field. We discuss implications for fabrication and performance of superconducting resonant frequency cavities in particle accelerators.

This study proposes a novel flexible hybrid state estimation (SE) algorithm when a realistic communication system with its irregularities is taken into account. This system is modelled by the Network Simulator 2 software tool, which is also used to calculate communication delays and packet drop probabilities. Within this setup, the system observability can be predicted, and the proposed SE can decide between using the static SE (SSE) or the discrete Kalman filter plus SSE-based measurements and time alignment (Forecasting-aided SE). Flexible hybrid SE (FHSE) incorporates both phasor measurement units and supervisory control and data acquisition-based measurements, with different time stamps. The proposed FHSE with detailed modelling of the communication system is motivated by: (i) well-known issues in SSE (time alignment of the measurements, frequent un-observability for fixed SE time stamps etc.); and (ii) the need to model a realistic communication system (calculated communication delays and packet drop probabilities are a part of the proposed FHSE). Application of the proposed algorithm is illustrated for examples with time-varying bus load/generation on two IEEE test cases: 14-bus and 300-bus.

We describe a method for simultaneously identifying and reducing dynamic power systems models in the form of differential-algebraic equations. Often, these models are large and complex, containing more parameters than can be identified from the available system measurements. We demonstrate our method on transient stability models, using the IEEE 14-bus test system.Ourapproachusestechniquesofinformationgeometryto remove unidentifiable parameters from the model. We examine the case of a networked system with 58 parameters using full observations throughout the network. We show that greater reduction can be achieved when only partial observations are available, including reduction of the network itself.

Model Boundary Approximation Method as a Unifying Framework for Balanced Truncation and Singular Perturbation Approximation

This paper describes a manifold learning algorithm for big data classification and parameter identification in real-time operation of power systems. We assume a black-box setting, where only SCADA-based measurements at the point of interest are available. Data classification is based on diffusion maps, where an improved data-informed metric construction for partition trees is used. Data reduction is demonstrated on an hourly measurement tensor example, collected from the power flow solutions calculated for daily load/generation profiles. Parameter identification is performed on the same example, generated via randomly selected input parameters. The proposed method is illustrated on the case of the static part (ZIP) of a detailed WECC load model, connected to a single bus of a real-world 441-bus power system.

Background: In systems biology, the dynamics of biological networks are often modeled with ordinary differential equations (ODEs) that encode interacting components in the systems, resulting in highly complex models. In contrast, the amount of experimentally available data is almost always limited, and insufficient to constrain the parameters. In this situation, parameter estimation is a very challenging problem. To address this challenge, two intuitive approaches are to perform experimental design to generate more data, and to perform model reduction to simplify the model. Experimental design and model reduction have been traditionally viewed as two distinct areas, and an extensive literature and excellent reviews exist on each of the two areas. Intriguingly, however, the intrinsic connections between the two areas have not been recognized.

Results: Experimental design and model reduction are deeply related, and can be considered as one unified framework. There are two recent methods that can tackle both areas, one based on model manifold and the other based on profile likelihood. We use a simple sum-of-two-exponentials example to discuss the concepts and algorithmic details of both methods, and provide Matlab-based code and implementation which are useful resources for the dissemination and adoption of experimental design and model reduction in the biology community.

Conclusions: From a geometric perspective, we consider the experimental data as a point in a high-dimensional data space and the mathematical model as a manifold living in this space. Parameter estimation can be viewed as a projection of the data point onto the manifold. By examining the singularity around the projected point on the manifold, we can perform both experimental design and model reduction. Experimental design identifies new experiments that expand the manifold and remove the singularity, whereas model reduction identifies the nearest boundary, which is the nearest singularity that suggests an appropriate form of a reduced model. This geometric interpretation represents one step toward the convergence of experimental design and model reduction as a unified framework.

The aim of this work is to develop calorimetric methods for characterizing the activity and stability of membrane immobilized enzymes. Invertase immobilized on a nylon-6 nanofiber membrane is used as a test case. The stability of both immobilized and free invertase activity was measured by spectrophotometry and isothermal titration calorimetry (ITC). Differential scanning calorimetry was used to measure the thermal stability of the structure and areal concentration of invertase on the membrane. This is the 1st demonstration that ITC can be used to determine activity and stability of an enzyme immobilized on a membrane. ITC and spectrophotometry show maximum activity of free and immobilized invertase at pH 4.5 and 45 to 55 °C. ITC determination of the activity as a function of temperature over an 8-h period shows a similar decline of activity of both free and immobilized invertase at 55 °C.

The paper proposes a power system state estimation algorithm in the presence of irregular sensor sampling and random communication delays. Our state estimator incorporates Phasor Measurement Units (PMU) and SCADA measurements. We use an Extended Kalman filter based algorithm for time alignment of measurements and state variables. Time stamps are assumed for PMU, SCADA and state estimation. Application of the proposed algorithm is illustrated for hourly/daily load/generation variations on two test examples: 14-bus and 118-bus.

Theoretical limits to the performance of superconductors in high magnetic fields parallel to their surfaces are of key relevance to current and future accelerating cavities, especially those made of new higher-Tc materials such as Nb3Sn, NbN, and MgB2. Indeed, beyond the so-called superheating field , flux will spontaneously penetrate even a perfect superconducting surface and ruin the performance. We present intuitive arguments and simple estimates for , and combine them with our previous rigorous calculations, which we summarize. We briefly discuss experimental measurements of the superheating field, comparing to our estimates. We explore the effects of materials anisotropy and the danger of disorder in nucleating vortex entry. Will we need to control surface orientation in the layered compound MgB2? Can we estimate theoretically whether dirt and defects make these new materials fundamentally more challenging to optimize than niobium? Finally, we discuss and analyze recent proposals to use thin superconducting layers or laminates to enhance the performance of superconducting cavities. Flux entering a laminate can lead to so-called pancake vortices; we consider the physics of the dislocation motion and potential re-annihilation or stabilization of these vortices after their entry.

We explore the relationship among experimental design, parameter estimation, and systematic error in sloppy models. We show that the approximate nature of mathematical models poses challenges for experimental design in sloppy models. In many models of complex biological processes it is unknown what are the relevant physical mechanisms that must be included to explain system behaviors. As a consequence, models are often overly complex, with many practically unidentifiable parameters. Furthermore, which mechanisms are relevant/irrelevant vary among experiments. By selecting complementary experiments, experimental design may inadvertently make details that were ommitted from the model become relevant. When this occurs, the model will have a large systematic error and fail to give a good fit to the data. We use a simple hyper-model of model error to quantify a model’s discrepancy and apply it to two models of complex biological processes (EGFR signaling and DNA repair) with optimally selected experiments. We find that although parameters may be accurately estimated, the discrepancy in the model renders it less predictive than it was in the sloppy regime where systematic error is small. We introduce the concept of a sloppy system–a sequence of models of increasing complexity that become sloppy in the limit of microscopic accuracy. We explore the limits of accurate parameter estimation in sloppy systems and argue that identifying underlying mechanisms controlling system behavior is better approached by considering a hierarchy of models of varying detail rather than focusing on parameter estimation in a single model.

The purposes of this paper are (a) to examine the effect of calorimeter time constant (τ) on heat rate data from a single enzyme injection into substrate in an isothermal titration calorimeter (ITC), (b) to provide information that can be used to predict the optimum experimental conditions for determining the rate constant (k₂), Michaelis constant (K_M), and enthalpy change of the reaction (Δ_RH), and (c) to describe methods for evaluating these parameters. We find that K_M, k₂ and Δ_RH can be accurately estimated without correcting for the calorimeter time constant, τ, if (k₂E/K_M), where E is the total active enzyme concentration, is between 0.1/τ and 1/τ and the reaction goes to at least 99% completion. If experimental conditions are outside this domain and no correction is made for τ, errors in the inferred parameters quickly become unreasonable. A method for fitting single-injection data to the Michaelis–Menten or Briggs–Haldane model to simultaneously evaluate K_M, k₂, Δ_RH, and τ is described and validated with experimental data. All four of these parameters can be accurately inferred provided the reaction time constant (k₂E/K_M) is larger than 1/τ and the data include enzyme saturated conditions.

Nb₃Sn film coatings have the potential to drastically improve the accelerating performance of Nb superconducting radiofrequency (SRF) cavities in next-generation linear particle accelerators. Unfortunately, persistent Nb₃Sn stoichiometric material defects formed during fabrication limit the cryogenic operating temperature and accelerating gradient by nucleating magnetic vortices that lead to premature cavity quenching. The SRF community currently lacks a predictive model that can explain the impact of chemical and morphological properties of Nb₃Sn defects on vortex nucleation and maximum accelerating gradients. Both experimental and theoretical studies of the material and superconducting properties of the first 100 nm of Nb₃Sn surfaces are complicated by significant variations in the volume distribution and topography of stoichiometric defects. This work contains a coordinated experimental study with supporting simulations to identify how the observed chemical composition and morphology of certain Sn-rich and Sn-deficient surface defects can impact the SRF performance. Nb₃Sn films were prepared with varying degrees of stoichiometric defects, and the film surface morphologies were characterized. Both Sn-rich and Sn-deficient regions were identified in these samples. For Sn-rich defects, we focus on elemental Sn islands that are partially embedded into the Nb₃Sn film. Using finite element simulations of the time-dependent Ginzburg-Landau equations, we estimate vortex nucleation field thresholds at Sn islands of varying size, geometry, and embedment. We find that these islands can lead to significant SRF performance degradation that could not have been predicted from the ensemble stoichiometry alone. For Sn-deficient Nb₃Sn surfaces, we experimentally identify a periodic nanoscale surface corrugation that likely forms because of extensive Sn loss from the surface. Simulation results show that the surface corrugations contribute to the already substantial drop in the vortex nucleation field of Sn-deficient Nb₃Sn surfaces. This work provides a systematic approach for future studies to further detail the relationship between experimental Nb₃Sn growth conditions, stoichiometric defects, geometry, and vortex nucleation. These findings have technical implications that will help guide improvements to Nb₃Sn fabrication procedures. Our outlined experiment-informed theoretical methods can assist future studies in making additional key insights about Nb₃Sn stoichiometric defects that will help build the next generation of SRF cavities and support related superconducting materials development efforts.

Maximum entropy is an approach for obtaining posterior probability distributions of modeling parameters. This approach, based on a cost function that quantifies the data-model mismatch, relies on an estimate of an appropriate temperature. Selection of this ”statistical temperature” is related to estimating the noise covariance. A method for selecting the ”statistical temperature” is derived from analogies with statistical mechanics, including the equipartition theorem. Using the equipartition-theorem estimate, the statistical temperature can be obtained for a single data sample instead of via the ensemble approach used previously. Examples of how the choice of temperature impacts the posterior distributions are shown using a toy model. The examples demonstrate the impact of the choice of the temperature on the resulting posterior probability distributions and the advantages of using the equipartition-theorem approach for selecting the temperature.

This tutorial demonstrates the use of information geometry tools in analyzing environmental parameter sensitivities in underwater acoustics. Sensitivity analyses quantify how well data can constrain model parameters, with application to inverse problems like geoacoustic inversion. A review of examples of parameter sensitivity methods and their application to problems in underwater acoustics is given, roughly grouped into “local” and “non-local” methods. Local methods such as Fisher information and Cramér-Rao bounds have important connections to information geometry. Information Geometry combines the fields of information theory and differential geometry by interpreting a model as a Riemannian manifold, known as the model manifold, that encodes both local and global parameter sensitivities. As an example, 2-dimensional model manifold slices are constructed for the Pekeris waveguide with sediment attenuation, for a vertical array of hydrophones. This example demonstrates how effective, reduced-order models emerge in certain parameter limits, which correspond to boundaries of the model manifold. This example also demonstrates how the global structure of the model manifold influences the local sensitivities quantified by the Fisher information matrix. This paper motivates future work to utilize information geometry methods for experimental design and model reduction applied to more complex modeling scenarios in underwater acoustics.

In this work, deep neural networks are trained on synthetic spectrograms of transiting ships to find properties of the seafloor and uncertainty labels associated with those predictions. The spectrograms are labeled with the values of sediment layer thickness, sound speed, density, and attenuation; and a measure of the parameter information content or sensitivity for each parameter obtained from the Cramér-Rao bound (CRB). The CRB values for a given ocean environment and source-receiver geometry can be calculated and expressed as a relative uncertainty, for each sediment property. To obtain uncertainty labels for each spectrogram, the relative CRB is calculated for ten equally spaced frequencies for each sediment parameter of interest. These relative CRB values are divided into uncertainty classes, and the mode class across frequency is assigned as the uncertainty label for the spectrogram. The labeled synthetic spectrograms are used to train ResNet-18 networks, which can then tested on measured spectrograms. Comparisons are made between validation performance of networks that are trained to learn only the parameter value labels and those trained to learn both seabed parameter values and sensitivity class. The validation results indicate the potential to predict not only sediment properties but uncertainty in those predictions.

The National Transportation Noise Map predicts time-averaged road traffic noise across the continental United States (CONUS) based on annual average daily traffic counts. However, traffic noise can vary greatly with time. This paper outlines a method for predicting nationwide hourly varying source traffic sound emissions called the Vehicular Reduced-Order Observation-based Model (VROOM). The method incorporates three models that predict temporal variability of traffic volume, predict temporal variability of different traffic classes, and use Traffic Noise Model (TNM) 3.0 equations to give traffic noise emission levels based on vehicle numbers and class mix. Location-specific features are used to predict average class mix across CONUS. VROOM then incorporates dynamic traffic class mix data to obtain dynamic traffic class mix. TNM 3.0 equations then give estimated equivalent sound level emission spectra near roads with up to hourly resolution. Important temporal traffic noise characteristics are modeled, including diurnal traffic patterns, rush hours in urban locations, and weekly and yearly variation. Examples of the temporal variability are depicted and possible types of uncertainties are identified. Altogether, VROOM can be used to map national transportation noise with temporal and spectral variability.

The model manifold, an information geometry tool, is a geometric representation of a model that can quantify the expected information content of modeling parameters. For a normal-mode sound propagation model in a shallow ocean environment, transmission loss (TL) is calculated for a vertical line array and model manifolds are constructed for both absolute and relative TL. For the example presented in this paper, relative TL yields more compact model manifolds with seabed environments that are less statistically distinguishable than manifolds of absolute TL. This example illustrates how model manifolds can be used to improve experimental design for inverse problems.

We develop information-geometric techniques to analyze the trajectories of the predictions of deep networks during training. By examining the underlying highdimensional probabilistic models, we reveal that the training process explores an effectively low-dimensional manifold. Networks with a wide range of architectures, sizes, trained using different optimization methods, regularization techniques, data augmentation techniques, and weight initializations lie on the same manifold in the prediction space. We study the details of this manifold to find that networks with different architectures follow distinguishable trajectories, but other factors have a minimal influence; larger networks train along a similar manifold as that of smaller networks, just faster; and networks initialized at very different parts of the prediction space converge to the solution along a similar manifold.

Separating crowd responses from raw acoustic signals at sporting events is challenging because recordings contain complex combinations of acoustic sources, including crowd noise, music, individual voices, and public address (PA) systems. This paper presents a data-driven decomposition of recordings of 30 collegiate sporting events. The decomposition uses machine-learning methods to find three principal spectral shapes that separate various acoustic sources. First, the distributions of recorded one-half-second equivalent continuous sound levels from men's and women's basketball and volleyball games are analyzed with regard to crowd size and venue. Using 24 one-third-octave bands between 50 Hz and 10 kHz, spectrograms from each type of game are then analyzed. Based on principal component analysis, 87.5% of the spectral variation in the signals can be represented with three principal components, regardless of sport, venue, or crowd composition. Using the resulting three-dimensional component coefficient representation, a Gaussian mixture model clustering analysis finds nine different clusters. These clusters separate audibly distinct signals and represent various combinations of acoustic sources, including crowd noise, music, individual voices, and the PA system.

Bifurcation phenomena are common in multidimensional multiparameter dynamical systems. Normal form theory suggests that bifurcations are driven by relatively few combinations of parameters. Models of complex systems, however, rarely appear in normal form, and bifurcations are controlled by nonlinear combinations of the bare parameters of differential equations. Discovering reparameterizations to transform complex equations into a normal form is often very difficult, and the reparameterization may not even exist in a closed form. Here we show that information geometry and sloppy model analysis using the Fisher information matrix can be used to identify the combination of parameters that control bifurcations. By considering observations on increasingly long timescales, we find those parameters that rapidly characterize the system's topological inhomogeneities, whether the system is in normal form or not. We anticipate that this novel analytical method, which we call time-widening information geometry (TWIG), will be useful in applied network analysis.

Bifurcation phenomena are common in multidimensional multiparameter dynamical systems. Normal form theory suggests that bifurcations are driven by relatively few combinations of parameters. Models of complex systems, however, rarely appear in normal form, and bifurcations are controlled by nonlinear combinations of the bare parameters of differential equations. Discovering reparameterizations to transform complex equations into a normal form is often very difficult, and the reparameterization may not even exist in a closed form. Here we show that information geometry and sloppy model analysis using the Fisher information matrix can be used to identify the combination of parameters that control bifurcations. By considering observations on increasingly long timescales, we find those parameters that rapidly characterize the system's topological inhomogeneities, whether the system is in normal form or not. We anticipate that this novel analytical method, which we call time-widening information geometry (TWIG), will be useful in applied network analysis.

The National Transportation Noise Map (NTNM) gives time-averaged traffic noise across the continental United States (CONUS) using annual average daily traffic. However, traffic noise varies significantly with time. This paper outlines the development and utility of a traffic volume model which is part of VROOM, the Vehicular Reduced-Order Observation-based model, which, using hourly traffic volume data from thousands of traffic monitoring stations across CONUS, predicts nationwide hourly varying traffic source noise. Fourier analysis finds daily, weekly, and yearly temporal traffic volume cycles at individual traffic monitoring stations. Then, principal component analysis uses denoised Fourier spectra to find the most widespread cyclic traffic patterns. VROOM uses nine principal components to represent hourly traffic characteristics for any location, encapsulating daily, weekly, and yearly variation. The principal component coefficients are predicted across CONUS using location-specific features. Expected traffic volume model sound level errors—obtained by comparing predicted traffic counts to measured traffic counts—and expected NTNM-like errors, are presented. VROOM errors are typically within a couple of decibels, whereas NTNM-like errors are often inaccurate, even exceeding 10 decibels. This work details the first steps towards creation of a temporally and spectrally variable national transportation noise map.

When multiple individuals interact in a conversation or as part of a large crowd, emergent structures and dynamics arise that are behavioral properties of the interacting group rather than of any individual member of that group. Recent work using traditional signal processing techniques and machine learning has demonstrated that global acoustic data recorded from a crowd at a basketball game can be used to classify emergent crowd behavior in terms of the crowd's purported emotional state. We propose that the description of crowd behavior from such global acoustic data could benefit from nonlinear analysis methods derived from dynamical systems theory. Such methods have been used in recent research applying nonlinear methods to audio data extracted from music and group musical interactions. In this work, we used nonlinear analyses to extract features that are relevant to the behavioral interactions that underlie acoustic signals produced by a crowd attending a sporting event. We propose that recurrence dynamics measured from these audio signals via recurrence quantification analysis (RQA) reflect information about the behavioral dynamics of the crowd itself. We analyze these dynamics from acoustic signals recorded from crowds attending basketball games, and that were manually labeled according to the crowds' emotional state across six categories: angry noise, applause, cheer, distraction noise, positive chant, and negative chant. We show that RQA measures are useful to differentiate the emergent acoustic behavioral dynamics between these categories, and can provide insight into the recurrence patterns that underlie crowd interactions.

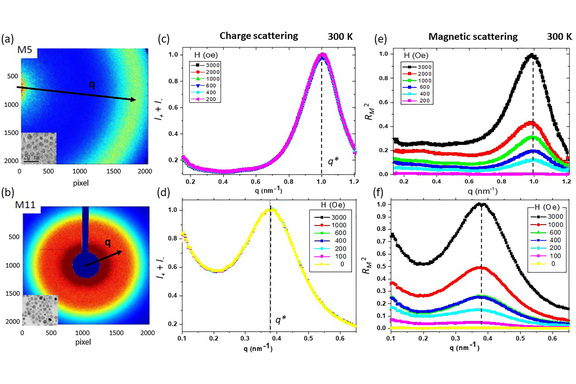
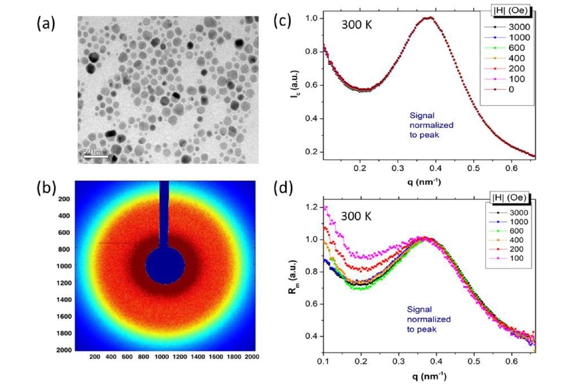
We report on magnetic orderings of nanospins in self-assemblies of Fe₃O₄ nanoparticles (NPs), occurring at various stages of the magnetization process throughout the superparamagnetic (SPM)-blocking transition. Essentially driven by magnetic dipole couplings and by Zeeman interaction with a magnetic field applied out-of-plane, these magnetic orderings include a mix of long-range parallel and antiparallel alignments of nanospins, with the antiparallel correlation being the strongest near the coercive point below the blocking temperature. The magnetic ordering is probed via x-ray resonant magnetic scattering (XRMS), with the x-ray energy tuned to the Fe−L₃ edge and using circular polarized light. By exploiting dichroic effects, a magnetic scattering signal is isolated from the charge scattering signal. We measured the nanospin ordering for two different sizes of NPs, 5 and 11 nm, with blocking temperatures TB of 28 and 170 K, respectively. At 300 K, while the magnetometry data essentially show SPM and absence of hysteresis for both particle sizes, the XRMS data reveal the presence of nonzero (up to 9%) antiparallel ordering when the applied field is released to zero for the 11 nm NPs. These antiparallel correlations are drastically amplified when the NPs are cooled down below TB and reach up to 12% for the 5 nm NPs and 48% for the 11 nm NPs, near the coercive point. The data suggest that the particle size affects the prevalence of the antiparallel correlations over the parallel correlations by a factor ∼1.6 to 3.8 higher when the NP size increases from 5 to 11 nm.

Modeling environmental sound levels over continental scales is difficult due to the variety of geospatial environments. Moreover, current continental-scale models depend upon machine learning and therefore face additional challenges due to limited acoustic training data. In previous work, an ensemble of machine learning models was used to predict environmental sound levels in the contiguous United States using a training set composed of 51 geospatial layers (downselected from 120) and acoustic data from 496 geographic sites from Pedersen, Transtrum, Gee, Lympany, James, and Salton [JASA Express Lett. 1(12), 122401 (2021)]. In this paper, the downselection process, which is based on factors such as data quality and inter-feature correlations, is described in further detail. To investigate additional dimensionality reduction, four different feature selection methods are applied to the 51 layers. Leave-one-out median absolute deviation cross-validation errors suggest that the number of geospatial features can be reduced to 15 without significant degradation of the model's predictive error. However, ensemble predictions demonstrate that feature selection results are sensitive to variations in details of the problem formulation and, therefore, should elicit some skepticism. These results suggest that more sophisticated dimensionality reduction techniques are necessary for problems with limited training data and different training and testing distributions.

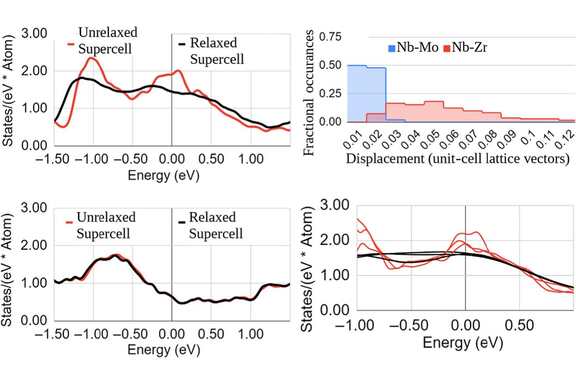
Superconducting radio-frequency (SRF) cavities currently rely on niobium (Nb), and could benefit from a higher-Tc surface, which would enable a higher operating temperature, lower surface resistance, and higher maximum fields. Surface zirconium (Zr) doping is one option for improvement, which has not previously been explored, likely because bulk alloy experiments showed only mild Tc enhancements of 1–2 K relative to Nb. Our ab initio results reveal a more nuanced picture: an ideal bcc Nb-Zr alloy would have Tc over twice that of niobium, but displacements of atoms away from the high-symmetry bcc positions due to the Jahn-Teller-Peierls effect almost completely eliminates this enhancement in typical disordered alloy structures. Ordered Nb-Zr alloy structures, in contrast, are able to avoid these atomic displacements and achieve higher calculated Tc up to a theoretical limit of 17.7 K. Encouraged by this, we tested two deposition methods: a physical-vapor Zr deposition method, which produced Nb-Zr surfaces with Tc values of 13.5 K, and an electrochemical deposition method, which produced surfaces with a possible 16-K Tc. An rf test of the highest-Tc surface showed a mild reduction in BCS surface resistance relative to Nb, demonstrating the potential value of this material for RF devices. Finally, our Ginzburg-Landau theory calculations show that realistic surface doping profiles should be able to reach the maximum rf fields necessary for next-generation applications, such as the ground-breaking LCLS-II accelerator. Considering the advantages of Nb-Zr compared to other candidate materials such as Nb3Sn and Nb-Ti-N, including a simple phase diagram with relatively little sensitivity to composition, and a stable, insulating ZrO2 native oxide, we conclude that Nb-Zr alloy is an excellent candidate for next-generation, high-quality-factor superconducting rf devices.

Applying machine learning methods to geographic data provides insights into spatial patterns in the data as well as assists in interpreting and describing environments. This paper investigates the results of k-means clustering applied to 51 geospatial layers, selected and scaled for a model of outdoor acoustic environments, in the continental United States. Silhouette and elbow analyses were performed to identify an appropriate number of clusters (eight). Cluster maps are shown and the clusters are described, using correlations between the geospatial layers and clusters to identify distinguishing characteristics for each cluster. A subclustering analysis is presented in which each of the original eight clusters is further divided into two clusters. Because the clustering analysis used geospatial layers relevant to modeling outdoor acoustics, the geospatially distinct environments corresponding to the clusters may aid in characterizing acoustically distinct environments. Therefore, the clustering analysis can guide data collection for the problem of modeling outdoor acoustic environments by identifying poorly sampled regions of the feature space (i.e., clusters which are not well-represented in the training data).

Superconducting radio-frequency (SRF) resonators are critical components for particle accelerator applications, such as free-electron lasers, and for emerging technologies in quantum computing. Developing advanced materials and their deposition processes to produce RF superconductors that yield n & omega; surface resistances is a key metric for the wider adoption of SRF technology. Here, ZrNb(CO) RF superconducting films with high critical temperatures (T-c) achieved for the first time under ambient pressure are reported. The attainment of a T-c near the theoretical limit for this material without applied pressure is promising for its use in practical applications. A range of T-c, likely arising from Zr doping variation, may allow a tunable superconducting coherence length that lowers the sensitivity to material defects when an ultra-low surface resistance is required. The ZrNb(CO) films are synthesized using a low-temperature (100 - 200 & DEG;C) electrochemical recipe combined with thermal annealing. The phase transformation as a function of annealing temperature and time is optimized by the evaporated Zr-Nb diffusion couples. Through phase control, one avoids hexagonal Zr phases that are equilibrium-stable but degrade T-c. X-ray and electron diffraction combined with photoelectron spectroscopy reveal a system containing cubic & beta;-ZrNb mixed with rocksalt NbC and low-dielectric-loss ZrO2. Proof-of-concept RF performance of ZrNb(CO) on an SRF sample test system is demonstrated. BCS resistance trends lower than reference Nb, while quench fields occur at approximately 35 mT. The results demonstrate the potential of ZrNb(CO) thin films for particle accelerators and other SRF applications.

Despite being so pervasive, road traffic noise can be difficult to model and predict on a national scale. Detailed road traffic noise predictions can be made on small geographic scales using the US Federal Highway Administration's Traffic Noise Model (TNM), but TNM becomes infeasible for the typical user on a nationwide scale because of the complexity and computational cost. Incorporating temporal and spectral variability also greatly increases complexity. To address this challenge, physics-based models are made using reported hourly traffic counts at locations across the country together with published traffic trends. Using these models together with TNM equations for spectral source emissions, a streamlined app has been created to efficiently predict traffic noise at roads across the nation with temporal and spectral variability. This app, which presently requires less than 700 MB of stored geospatial data and models, incorporates user inputs such as location, time period, and frequency, and gives predicted spectral levels within seconds.

Sensitivity analysis is a powerful tool for analyzing multi-parameter models. For example, the Fisher information matrix (FIM) and the Cramer-Rao bound (CRB) involve derivatives of a forward model with respect to parameters. However, these derivatives are difficult to estimate in ocean acoustic models. This work presents a frequency-agnostic methodology for accurately estimating numerical derivatives using physics-based parameter preconditioning and Richardson extrapolation. The methodology is validated on a case study of transmission loss in the 50-400Hz band from a range-independent normal mode model for parameters of the sediment. Results demonstrate the utility of this methodology for obtaining Cramer-Rao bound (CRB) related to both model sensitivities and parameter uncertainties, which reveal parameter correlation in the model. This methodology is a general tool that can inform model selection and experimental design for inverse problems in different applications.

Complex models in physics, biology, economics, and engineering are often sloppy, meaning that the model parameters are not well determined by the model predictions for collective behavior. Many parameter combinations can vary over decades without significant changes in the predictions. This review uses information geometry to explore sloppiness and its deep relation to emergent theories. We introduce the model manifold of predictions, whose coordinates are the model parameters. Its hyperribbon structure explains why only a few parameter combinations matter for the behavior. We review recent rigorous results that connect the hierarchy of hyperribbon widths to approximation theory, and to the smoothness of model predictions under changes of the control variables. We discuss recent geodesic methods to find simpler models on nearby boundaries of the model manifold-emergent theories with fewer parameters that explain the behavior equally well. We discuss a Bayesian prior which optimizes the mutual information between model parameters and experimental data, naturally favoring points on the emergent boundary theories and thus simpler models. We introduce a 'projected maximum likelihood' prior that efficiently approximates this optimal prior, and contrast both to the poor behavior of the traditional Jeffreys prior. We discuss the way the renormalization group coarse-graining in statistical mechanics introduces a flow of the model manifold, and connect stiff and sloppy directions along the model manifold with relevant and irrelevant eigendirections of the renormalization group. Finally, we discuss recently developed 'intensive' embedding methods, allowing one to visualize the predictions of arbitrary probabilistic models as low-dimensional projections of an isometric embedding, and illustrate our method by generating the model manifold of the Ising model.

The National Transportation Noise Map predicts time-averaged road traffic noise across the continental United States (CONUS) based on average annual daily traffic counts. However, traffic counts may vary significantly with time. Since traffic noise is correlated with traffic counts, a more detailed temporal representation of traffic noise requires knowledge of the time-varying traffic counts. Each year, the Federal Highway Administration tabulates the hourly traffic counts recorded at more than 5000 traffic monitoring sites across CONUS. Each site records up to 8760 traffic counts corresponding to each hour of the year. The hourly traffic counts can be treated as time-dependent signals upon which signal processing techniques can be applied. First, Fourier analysis is used to find the daily, weekly, and yearly temporal cycles present at each traffic monitoring site. Next, principal component analysis is applied to the peaks in the Fourier spectra. A reduced-order model using only nine principal components represents much of the temporal variability in traffic counts while requiring only 0.1% as many values as the original hourly traffic counts. This reduced-order model can be used in conjunction with sound mapping tools to predict traffic noise on hourly, rather than time-averaged, timescales. [Work supported by U.S. Army SBIR.]

We consider how mathematical models enable predictions for conditions that are qualitatively different from the training data. We propose techniques based on information topology to find models that can apply their learning in regimes for which there is no data. The first step is to use the manifold boundary approximation method to construct simple, reduced models of target phenomena in a data-driven way. We consider the set of all such reduced models and use the topological relationships among them to reason about model selection for new, unobserved phenomena. Given minimal models for several target behaviors, we introduce the supremum principle as a criterion for selecting a new, transferable model. The supremal model, i.e., the least upper bound, is the simplest model that reduces to each of the target behaviors. We illustrate how to discover supremal models with several examples; in each case, the supremal model unifies causal mechanisms to transfer successfully to new target domains. We use these examples to motivate a general algorithm that has formal connections to theories of analogical reasoning in cognitive psychology.

The synthesis of new proteins and the degradation of old proteins in vivo can be quantified in serial samples using metabolic isotope labeling to measure turnover. Because serial biopsies in humans are impractical, we set out to develop a method to calculate the turnover rates of proteins from single human biopsies. This method involved a new metabolic labeling approach and adjustments to the calculations used in previous work to calculate protein turnover. We demonstrate that using a nonequilibrium isotope enrichment strategy avoids the time dependent bias caused by variable lag in label delivery to different tissues observed in traditional metabolic labeling methods. Turnover rates are consistent for the same subject in biopsies from different labeling periods, and turnover rates calculated in this study are consistent with previously reported values. We also demonstrate that by measuring protein turnover we can determine where proteins are synthesized. In human subjects a significant difference in turnover rates differentiated proteins synthesized in the salivary glands versus those imported from the serum. We also provide a data analysis tool, DeuteRater-H, to calculate protein turnover using this nonequilibrium metabolic ²H₂O method.

In this paper, we consider the problem of quantifying parametric uncertainty in classical empirical interatomic potentials (IPs) using both Bayesian (Markov Chain Monte Carlo) and frequentist (profile likelihood) methods. We interface these tools with the Open Knowledgebase of Interatomic Models and study three models based on the Lennard-Jones, Morse, and Stillinger-Weber potentials. We confirm that IPs are typically sloppy, i.e., insensitive to coordinated changes in some parameter combinations. Because the inverse problem in such models is ill-conditioned, parameters are unidentifiable. This presents challenges for traditional statistical methods, as we demonstrate and interpret within both Bayesian and frequentist frameworks. We use information geometry to illuminate the underlying cause of this phenomenon and show that IPs have global properties similar to those of sloppy models from fields, such as systems biology, power systems, and critical phenomena. IPs correspond to bounded manifolds with a hierarchy of widths, leading to low effective dimensionality in the model. We show how information geometry can motivate new, natural parameterizations that improve the stability and interpretation of uncertainty quantification analysis and further suggest simplified, less-sloppy models.

The article explores the analysis of transient phenomena in large-scale power systems subjected to major disturbances from the aspect of interleaving, coordinating, and refining physics- and data-driven models. Major disturbances can lead to cascading failures and ultimately to the partial power system blackout. Our primary interest is in a framework that would enable coordinated and seamlessly integrated use of the two types of models in engineered systems. Parts of this framework include: 1) optimized compressed sensing, 2) customized finite-dimensional approximations of the Koopman operator, and 3) gray-box integration of physics-driven (equation-based) and data-driven (deep neural network-based) models. The proposed three-stage procedure is applied to the transient stability analysis on the multimachine benchmark example of a 441-bus real-world test system, where the results are shown for a synchronous generator with local measurements in the connection point.

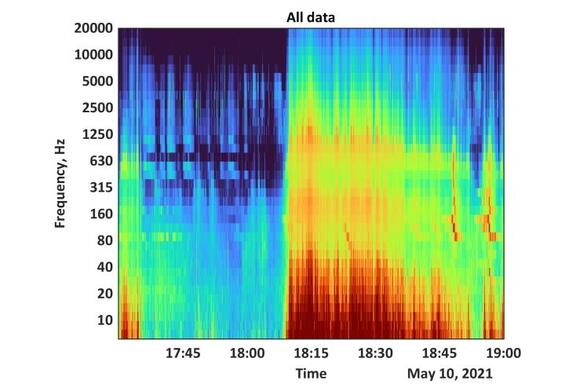
Wind-induced microphone self-noise is a non-acoustic signal that may contaminate outdoor acoustical measurements, particularly at low frequencies, even when using a windscreen. A recently developed method [Cook et al., JASA Express Lett. 1, 063602 (2021)] uses the characteristic spectral slope of wind noise in the inertial subrange for screened microphones to automatically classify and reduce wind noise in acoustical measurements in the lower to middling frequency range of human hearing. To explore its uses and limitations, this method is applied to acoustical measurements which include both natural and anthropogenic noise sources. The method can be applied to one-third octave band spectral data with different frequency ranges and sampling intervals. By removing the shorter timescale data at frequencies where wind noise dominates the signal, the longer timescale acoustical environment can be more accurately represented. While considerations should be made about the specific applicability of the method to particular datasets, the wind reduction method allows for simple classification and reduction of wind-noise-contaminated data in large, diverse datasets.

Crowd violence and the repression of free speech have become increasingly relevant concerns in recent years. This paper considers a new application of crowd control, namely, keeping the public safe during large scale demonstrations by anticipating the evolution of crowd emotion dynamics through state estimation. This paper takes a first step towards solving this problem by formulating a crowd state prediction problem in consideration of recent work involving crowd psychology and opinion modeling. We propose a nonlinear crowd behavior model incorporating parameters of agent personality, opinion, and relative position to simulate crowd emotion dynamics. This model is then linearized and used to build a state observer whose effectiveness is then tested on system outputs from both nonlinear and linearized models. We show that knowing the value of the equilibrium point for the full nonlinear system is a necessary condition for convergence of this class of estimators, but otherwise not much information about the crowd is needed to obtain good estimates. In particular, zero-error convergence is possible even when the estimator erroneously uses nominal or average personality parameters in its model for each member of the crowd.